
- Machine Learning Basics
- Machine Learning - Home
- Machine Learning - Getting Started
- Machine Learning - Basic Concepts
- Machine Learning - Python Libraries
- Machine Learning - Applications
- Machine Learning - Life Cycle
- Machine Learning - Required Skills
- Machine Learning - Implementation
- Machine Learning - Challenges & Common Issues
- Machine Learning - Limitations
- Machine Learning - Reallife Examples
- Machine Learning - Data Structure
- Machine Learning - Mathematics
- Machine Learning - Artificial Intelligence
- Machine Learning - Neural Networks
- Machine Learning - Deep Learning
- Machine Learning - Getting Datasets
- Machine Learning - Categorical Data
- Machine Learning - Data Loading
- Machine Learning - Data Understanding
- Machine Learning - Data Preparation
- Machine Learning - Models
- Machine Learning - Supervised
- Machine Learning - Unsupervised
- Machine Learning - Semi-supervised
- Machine Learning - Reinforcement
- Machine Learning - Supervised vs. Unsupervised
- Machine Learning Data Visualization
- Machine Learning - Data Visualization
- Machine Learning - Histograms
- Machine Learning - Density Plots
- Machine Learning - Box and Whisker Plots
- Machine Learning - Correlation Matrix Plots
- Machine Learning - Scatter Matrix Plots
- Statistics for Machine Learning
- Machine Learning - Statistics
- Machine Learning - Mean, Median, Mode
- Machine Learning - Standard Deviation
- Machine Learning - Percentiles
- Machine Learning - Data Distribution
- Machine Learning - Skewness and Kurtosis
- Machine Learning - Bias and Variance
- Machine Learning - Hypothesis
- Regression Analysis In ML
- Machine Learning - Regression Analysis
- Machine Learning - Linear Regression
- Machine Learning - Simple Linear Regression
- Machine Learning - Multiple Linear Regression
- Machine Learning - Polynomial Regression
- Classification Algorithms In ML
- Machine Learning - Classification Algorithms
- Machine Learning - Logistic Regression
- Machine Learning - K-Nearest Neighbors (KNN)
- Machine Learning - Naïve Bayes Algorithm
- Machine Learning - Decision Tree Algorithm
- Machine Learning - Support Vector Machine
- Machine Learning - Random Forest
- Machine Learning - Confusion Matrix
- Machine Learning - Stochastic Gradient Descent
- Clustering Algorithms In ML
- Machine Learning - Clustering Algorithms
- Machine Learning - Centroid-Based Clustering
- Machine Learning - K-Means Clustering
- Machine Learning - K-Medoids Clustering
- Machine Learning - Mean-Shift Clustering
- Machine Learning - Hierarchical Clustering
- Machine Learning - Density-Based Clustering
- Machine Learning - DBSCAN Clustering
- Machine Learning - OPTICS Clustering
- Machine Learning - HDBSCAN Clustering
- Machine Learning - BIRCH Clustering
- Machine Learning - Affinity Propagation
- Machine Learning - Distribution-Based Clustering
- Machine Learning - Agglomerative Clustering
- Dimensionality Reduction In ML
- Machine Learning - Dimensionality Reduction
- Machine Learning - Feature Selection
- Machine Learning - Feature Extraction
- Machine Learning - Backward Elimination
- Machine Learning - Forward Feature Construction
- Machine Learning - High Correlation Filter
- Machine Learning - Low Variance Filter
- Machine Learning - Missing Values Ratio
- Machine Learning - Principal Component Analysis
- Machine Learning Miscellaneous
- Machine Learning - Performance Metrics
- Machine Learning - Automatic Workflows
- Machine Learning - Boost Model Performance
- Machine Learning - Gradient Boosting
- Machine Learning - Bootstrap Aggregation (Bagging)
- Machine Learning - Cross Validation
- Machine Learning - AUC-ROC Curve
- Machine Learning - Grid Search
- Machine Learning - Data Scaling
- Machine Learning - Train and Test
- Machine Learning - Association Rules
- Machine Learning - Apriori Algorithm
- Machine Learning - Gaussian Discriminant Analysis
- Machine Learning - Cost Function
- Machine Learning - Bayes Theorem
- Machine Learning - Precision and Recall
- Machine Learning - Adversarial
- Machine Learning - Stacking
- Machine Learning - Epoch
- Machine Learning - Perceptron
- Machine Learning - Regularization
- Machine Learning - Overfitting
- Machine Learning - P-value
- Machine Learning - Entropy
- Machine Learning - MLOps
- Machine Learning - Data Leakage
- Machine Learning - Resources
- Machine Learning - Quick Guide
- Machine Learning - Useful Resources
- Machine Learning - Discussion
Machine Learning - Multiple Linear Regression
It is basically the extension of simple linear regression that predicts a response using two or more features. Mathematically we can explain it as follows −
Consider a dataset having n observations, p features i.e. independent variables and y as one response i.e. dependent variable the regression line for p features can be calculated as follows −
h(xi)=b0+b1xi1+b2xi2+⋅⋅⋅+bpxip
Here,h(xi) is the predicted response value and b0,b1,b2....bp are the regression coefficients.
Multiple Linear Regression models always includes the errors in the data known as residual error which changes the calculation as follows −
h(xi)=b0+b1xi1+b2xi2+⋅⋅⋅+bpxip+ei
We can also write the above equation as follows −
yi=h(xi)+eiorei=yi−h(xi)
Python Implementation
To implement multiple linear regression in Python using Scikit-Learn, we can use the same LinearRegression class as in simple linear regression, but this time we need to provide multiple independent variables as input.
Let's consider the Boston Housing dataset from Scikit-Learn and implement multiple linear regression using it.
Example
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import numpy as np
import matplotlib.pyplot as plt
# Load the Boston Housing dataset
boston = load_boston()
# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(boston.data,
boston.target, test_size=0.2, random_state=0)
# Create a linear regression object
lr_model = LinearRegression()
# Fit the model on the training data
lr_model.fit(X_train, y_train)
# Make predictions on the test data
y_pred = lr_model.predict(X_test)
# Calculate the mean squared error
mse = mean_squared_error(y_test, y_pred)
# Calculate the coefficient of determination
r2 = r2_score(y_test, y_pred)
print('Mean Squared Error:', mse)
print('Coefficient of Determination:', r2)
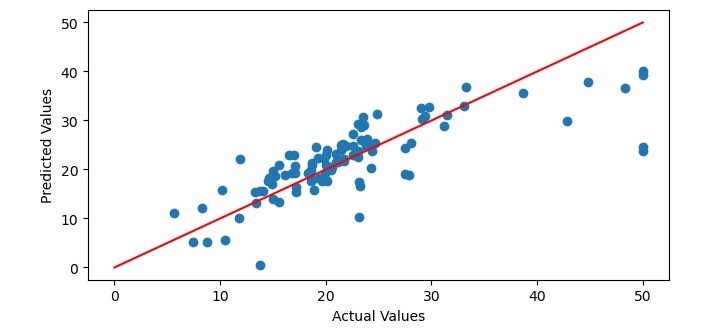
# Plot the predicted values against the actual values
plt.figure(figsize=(7.5, 3.5))
plt.scatter(y_test, y_pred)
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
# Add a regression line to the plot
x = np.linspace(0, 50, 100)
y = x
plt.plot(x, y, color='red')
# Show the plot
plt.show()
In this code, we first load the Boston Housing dataset using the load_boston() function from Scikit-Learn. We then split the dataset into training and testing sets using the train_test_split() function.
Next, we create a LinearRegression object and fit it on the training data using the fit() method. We then make predictions on the test data using the predict() method and calculate the mean squared error and coefficient of determination using the mean_squared_error() and r2_score() functions, respectively.
Finally, we plot the predicted values against the actual values using the scatter() function and add a regression line to the plot using the plot() function. We label the x-axis and y-axis using the xlabel() and ylabel() functions and display the plot using the show() function.
Output
When you execute the program, it will produce the following plot as the output and it will print the Mean Squared Error and the Coefficient of Determination on the terminal −
Mean Squared Error: 33.44897999767653 Coefficient of Determination: 0.5892223849182507
To Continue Learning Please Login